arXiv:0906.0060v5 [cs.SI] 17 Jun 2011
A Walk in Facebook: Uniform Sampling of Users
in Online Social Networks
Minas Gjoka
CalIT2
UC Irvine
Maciej Kurant
CalIT2
UC Irvine
Carter T. Butts
Sociology Dept
UC Irvine
buttsc@uci.edu
Athina Markopoulou
EECS Dept
UC Irvine
Abstract—Our goal in this paper is to develop a practical
framework for obtaining a uniform sample of users in an online
social network (OSN) by crawling its social graph. Such a
sample allows to estimate any user property and some topological
properties as well. To this end, first, we consider and compare
several candidate crawling techniques. Two approaches that can
produce approximately uniform samples are the Metropolis-
Hasting random walk (MHRW) and a re-weighted random walk
(RWRW). Both have pros and cons, which we demonstrate
through a comparison to each other as well as to the “ground
truth.” In contrast, using Breadth-First-Search (BFS) or an unad-
justed Random Walk (RW) leads to substantially biased results.
Second, and in addition to offline performance assessment, we
introduce online formal convergence diagnostics to assess sample
quality during the data collection process. We show how these
diagnostics can be used to effectively determine when a random
walk sample is of adequate size and quality. Third, as a case
study, we apply the above methods to Facebook and we collect
the first, to the best of our knowledge, representative sample of
Facebook users. We make it publicly available and employ it
to characterize several key properties of Facebook.
Index Terms—Sampling methods, Social network services,
Facebook, Random Walks, Convergence, Measurements, Graph
sampling.
I. INTRODUCTION
Online Social Networks (OSNs) have recently emerged as
a new Internet “killer-application.” The adoption of OSNs by
Internet users is off-the-charts with respect to almost every
metric. In November 2010, Facebook, the most popular
OSN, counted more than 500 million members; the total
combined membership in the top five OSNs (Facebook,
QQ, Myspace, Orkut, Twitter) exceeded 1 billion users.
Putting this number into context, the population of OSN users
is approaching 20% of the world population and is more than
50% of the world’s Internet users. According to Nielsen [1],
users worldwide currently spend over 110 billion minutes on
social media sites per month, which accounts for 22% of
all time spent online, surpassing even time spent on email.
According to Alexa [2], a well-known traffic analytics website,
Facebook is the second most visited website on the Internet
(second only to Google) with each user spending 30 minutes
on average per day on the site (more than the time spent
on Google). Four of the top five OSNs are also contained in
Alexa’s top 15 websites in regard to traffic rankings. Clearly,
OSNs in general, and Facebook in particular, have become
an important phenomenon on the Internet.
OSNs are of interest to several different communities. For
example, sociologists employ them as a venue for collecting
relational data and studying online human behavior. Marketers,
by contrast, seek to exploit information about OSNs in the
design of viral marketing strategies. From an engineering
perspective, understanding OSNs can enable the design of
better networked systems. For example, an OSN provider
may want to understand the social graph and user activity in
order to improve user experience by optimizing the design
of their datacenters and/or data storage on the cloud [3];
or by providing personalized services and ads. A network
provider may also want to understand the traffic generated by
activities of OSN users in order to design mechanisms, such
as caching [4] and traffic engineering [5], to better serve that
traffic.
Another potential use of OSNs is in algorithms that employ
trusted or influential users, e.g., to thwart unwanted commu-
nication while not impeding legitimate communication [6]; to
utilize social trust for collaborative spam filtering [7]; or to en-
able online personas to cost-effectively obtain credentials [8].
Third-party applications are also interested in OSNs in order
to provide personalized services as well as to become popular.
The immense interest generated by OSNs has given rise
to a number of measurement and characterization studies that
attempt to provide a first step towards their understanding.
Only a very small number of these studies are based on
complete datasets provided by the OSN operators [9,10]. A
few other studies have collected a complete view of specific
parts of OSNs; e.g., [11] collected the social graph of the
Harvard university network. However, the complete dataset
is typically unavailable to researchers, as most OSNs are
unwilling to share their company’s data even in an anonymized
form, primarily due to privacy concerns.
Furthermore, the large size
1
and access limitations of most
1
A back-of-the-envelope calculation of the effort needed to crawl
Facebook’s social graph is as follows. In December 2010, Facebook
advertised more than 500 million active users, each encoded by 64 bits (4
bytes) long userID, and 130 friends per user on average. Therefore, the
raw topological data alone, without any node attributes, amounts to at least
500M × 130 × 8 bytes ≃ 520 GBytes.
OSN services (e.g., login requirements, limited view, API
query limits) make it difficult or nearly impossible to fully
cover the social graph of an OSN. In many cases, HTML
scraping is necessary, which increases the overhead multifold.
2
Instead, it would be desirable to obtain and use a small but
representative sample.
Given this, sampling techniques are essential for practical
estimation of OSN properties. While sampling can, in princi-
ple, allow precise population-level inference from a relatively
small number of observations, this depends critically on the
ability to draw a sample with known statistical properties. The
lack of a sampling frame (i.e., a complete list of users, from
which individuals can be directly sampled) for most OSNs
makes principled sampling especially difficult. To elide this
limitation, our work focuses on sampling methods that are
based on crawling of friendship relations - a fundamental
primitive in any OSN.
Our goal in this paper is to provide a framework for
obtaining an asymptotically uniform sample (or one that can
be systematically reweighted to approach uniformity) of OSN
users by crawling the social graph. We provide practical
recommendations for appropriately implementing the frame-
work, including: the choice of crawling technique; the use
of online convergence diagnostics; and the implementation of
high-performance crawlers. We then apply our framework to
an important case-study - Facebook. More specifically, we
make the following three contributions.
Our first contribution is the comparison of several candidate
graph-crawling techniques in terms of sampling bias and
efficiency. First, we consider Breadth-First-Search (BFS) -
the most widely used technique for measuring OSNs [9,12]
including Facebook [13]. BFS sampling is known to in-
troduce bias towards high degree nodes, which is highly
non-trivial to characterize analytically [14,15] or to correct.
Second, we consider Random Walk (RW) sampling, which
also leads to bias towards high degree nodes, but whose bias
can be quantified by Markov Chain analysis and corrected via
appropriate re-weighting (RWRW) [16,17]. Then, we consider
the Metropolis-Hastings Random Walk (MHRW) that can
directly yield a uniform stationary distribution of users. This
technique has been used in the past for P2P sampling [18],
recently for a few OSNs [19,20], but not for Facebook.
Finally, we also collect a uniform sample of Facebook
userIDs (UNI), selected by a rejection sampling procedure
from Facebook’s 32-bit ID space, which serves as our
“ground truth”. We compare all sampling methods in terms
of their bias and convergence speed. We show that MHRW
and RWRW are both able to collect asymptotically uniform
samples, while BFS and RW result in a significant bias in
practice. We also compare the efficiency MHRW to RWRW,
via analysis, simulation and experimentation and discuss their
pros and cons. The former provides a sample ready to be
used by non-experts, while the latter is more efficient for all
2
For the example in footnote 1, one would have to download about 500M ×
230 KBytes ≃ 115 T Bytes of uncompressed HTML data.
practical purposes.
Our second contribution is that we introduce, for the first
time in this context, the use of formal convergence diagnostics
(namely Geweke and Gelman-Rubin) to assess sample quality
in an online fashion. These methods (adapted from Markov
Chain Monte Carlo applications) allow us to determine, in the
absence of a ground truth, when a sample is adequate for use,
and hence when it is safe to stop sampling. These is a critical
issue in implementation.
Our third contribution is that we apply and compare all the
aforementioned techniques for the first time, to the best of
our knowledge, on a large scale OSN. We use Facebook
as a case study by crawling its web front-end, which is
highly non-trivial due to various access limitations, and we
provide guidelines for the practical implementation of high-
performance crawlers. We obtain the first representative sam-
ple of Facebook users, which we make publicly avail-
able [21]; we have received approximately 500 requests for
this dataset in the last eighteen months. Finally, we use the
collected datasets to characterize several key properties of
Facebook, including user properties (e.g., privacy settings)
and topological properties (e.g., the node degree distribution,
clustering, and assortativity).
The structure of this paper is as follows. Section II discusses
related work. Section III describes the sampling methodol-
ogy, including the assumptions and limitations, the candi-
date crawling techniques and the convergence diagnostics.
Section IV describes the data collection process, including
the implementation of high-performance crawlers, and the
collected data sets from Facebook. Section V evaluates
and compares all sampling techniques in terms of efficiency
(convergence of various node properties) and quality (bias) of
the obtained sample. Section VI provides a characterization of
some key Facebook properties, based on the MHRW sample.
Section VII concludes the paper. The appendices elaborate
on the following points: (A) the uniform sample obtained
via userID rejection sampling, used as “ground truth” in this
paper; (B) the lack of temporal dynamics in Facebook, in the
timescale of our crawls; and (C) a comparison of the sampling
efficiency of MHRW vs. RWRW.
II. RELATED WORK
Broadly speaking, there are two bodies of work related to
this paper: (i) sampling techniques, investigating the quality
and efficiency of the sampling technique itself and (ii) charac-
terization studies, focusing on the properties of online social
networks based on the collected data. In this section, we review
this related literature and place our work in perspective.
A. Graph sampling techniques
Graph sampling techniques, via crawling, can be roughly
classified into two categories: graph traversal techniques and
random walks. In graph traversal techniques, nodes are sam-
pled without replacement: once a node is visited, it is not
visited again. These methods differ in the order in which they
visit the nodes; examples include Breadth-Search-First (BFS),
2
Depth-First Search (DFS), Forest Fire (FF) and Snowball
Sampling (SBS) [22].
BFS, in particular, is a basic technique that has been
used extensively for sampling OSNs in past research [9,12,
13,23,24]. One reason for this popularity is that an (even
incomplete) BFS sample collects a full view (all nodes and
edges) of some particular region in the graph. However, BFS
has been shown to lead to a bias towards high degree nodes
in various artificial and real world topologies [25]–[27]. Our
work also confirms the bias of BFS when sampling Online
Social Networks. It is worth noting that BFS and its variants
lead to samples that not only are biased but also do not
have known statistical properties (and hence cannot in general
be used to produce trustworthy estimates). Although recent
work suggests that it is possible to analytically compute
and correct this bias for random graphs with certain degree
distributions [14], these methods are mere heuristics under
arbitrary graphs [15] and will fail for networks with large-
scale heterogeneity (e.g., block structure).
Random walks on graphs are a well-studied topic; see [28]
for an excellent survey. They have been used for sampling the
World Wide Web (WWW) [29,30], peer-to-peer networks [17,
18,31], and other large graphs [32]. Similarly to traversals,
random walks are typically biased towards high-degree nodes.
However, the bias of random walks can be analyzed and
corrected for using classical results from Markov Chains. If
necessary, such a bias correction can be obtained during the
walk itself - the resulting Metropolis-Hasting Random Walk
(MHRW) described in Section III-C4 has been applied by
Stutzbach et al. [18] to select a representative sample of
peers in the Gnutella network. Alternatively, we can re-weight
the sample after it is collected - the resulting Re-Weighted
Random Walk (RWRW) described in Section III-C3 has been
recently compared with MHRW in the context of peer-to-peer
sampling by Rasti et al. [17]. Further improvements or variants
of random walks include random walk with jumps [29,33],
multiple dependent random walks [34], weighted random
walks [35], or multigraph sampling [36].
Our work is most closely related to the random walk
techniques. We obtain unbiased estimators of user properties
in Facebook using MHRW and RWRW and we compare the
two through experiments and analysis; BFS and RW (without
re-weighting) are used mainly as baselines for comparison.
We complement the crawling techniques with formal, online
convergence diagnostic tests using several node properties.To
the best of our knowledge, this has not been done before
in measurements of such systems. The closest to formal
diagnostics is the work by Latapy et al. [37] which studies
how the properties of interest evolve when the sample grows
to practically detect steady state. We also implement multiple
parallel chains. Multiple chains started at the same node have
been recently used in [17]. In contrast, we start different chains
from different nodes. We demonstrate that random walks,
whose bias can be analyzed and corrected, are able to estimate
properties of users in OSNs remarkably well in practice. We
also find that correcting for the bias at the end (RWRW),
rather than during the walk (MHRW) is more efficient for
all practical purposes - a finding that agrees with [17].
In terms of application, we apply the measurement tech-
niques to online social networks and study characteristics
specific to that context. To the best of our knowledge, we
are the first to obtain an unbiased sample of a large scale
OSN, namely Facebook, and make it publicly available.
Krishnamurthy et al. [20] ran a single Metropolis Random
Walk, inspired by [18], on Twitter as a way to verify the
lack of bias in their main crawl used throughout the paper.
However, the Metropolis algorithm was not the main focus
of their paper and Twitter is a directed graph which requires
different treatment. Parallel to our work, Rasti et al. [19] also
applied similar random walk techniques to collect unbiased
samples of Friendster.
Previous work on the temporal dynamics of social networks
includes [19,38]–[41]. Kumar et al. [38] studied the structure
and evolution of Flickr and Yahoo! from datasets provided by
the OSN providers. Backstrom et al. [39] presented different
ways in which communities in social networks grow over time
and [40] proposed a method for modeling relationships that
change over time in a social network. Willinger et al. [41] pro-
posed a multi-scale approach to study dynamic social graphs
at a coarser level of granularity. Rasti et al. [19] evaluate
the performance of random walks in dynamic graphs via
simulations and show that there is a tradeoff between number
of parallel samplers, churn and accuracy. In our work, we
assume that the social graph remains static during the crawl,
which we show in Appendix B to be the case for Facebook
in practice. Therefore, we do not consider dynamics, which
are essential in other sampling contexts.
A unique asset of our study is the collection of true
uniform sample of OSN users through rejection sampling of
userIDs (UNI), which served as ground truth in this paper; see
Section III-D. We note that UNI yields a uniform sample of
users regardless of the allocation policy of userIDs by the
OSN, as shown in Appendix A. UNI is essentially a star
random node sampling scheme [42]; this is different from the
induced subgraph random node sampling schemes that were
evaluated in [32,43].
B. Characterization studies of OSNs
Several papers have measured and characterized properties
of OSNs. In [44], Krishnamurthy presents a summary of
the challenges that researchers face in collecting data from
OSNs. In [9], Ahn et al. analyze three online social networks;
one complete social graph of Cyworld obtained from the
Cyworld provider, and two small samples from Orkut
and Myspace crawled with BFS. In [12,23], Mislove et al.
studied the properties of the social graph in four popular
OSNs: Flickr, LiveJournal, Orkut, and YouTube.
Their approach was to collect the large Weakly Connected
Component, also using BFS; their study shows that OSNs are
structurally different from other complex networks.
[11,13,45] are related to this paper in that they also study
Facebook. Wilson et al. [13] collect and analyze social
3
graphs and user interaction graphs in Facebook between
March and May 2008. Their methodology is what we refer
to as Region-Constrained BFS: they exhaustively collect all
open user profiles and their list of friends in the largest regional
networks. Such Region-Constrained BFS might be appropriate
to study particular regions, but it does not provide Facebook-
wide information, which is the goal of this paper. Furthermore,
the percentage of users in the social graph retrieved in [13] is
30%-60% less than the maximum possible in each network.
3
Our findings show some noteworthy differences from [13]: for
example, we find larger values of the degree-dependent clus-
tering coefficient, significantly higher assortativity coefficient,
and a degree distribution that does not follow a power law.
Finally, Wilson et al. [13] focus on the user interaction graph,
while we focus on the friendship graph. [11] and [45] have also
made publicly available and analyzed datasets corresponding
to university networks from Facebook with many annotated
properties for each student. In contrast, we collect a sample
of the global Facebook social graph.
Other works that have measured properties of Facebook
include [24,46]–[48]. In [46], Krishnamurthy et al. examine
the usage of privacy settings in Myspace and Facebook,
and the potential privacy leakage in OSNs. Compared to that
work, we have one common privacy attribute, “View friends“,
for which we observe similar results using our unbiased
sample. We also have additional privacy settings and the
one-hop neighborhood for every node, which allows us to
analyze user properties conditioned on their privacy awareness.
Bonneau et al. [47] demonstrate that many interesting user
properties can be accurately approximated just by crawling
“public search listings”.
Finally, there is a large body of work on the collection
and analysis of datasets for platforms or services that are
not pure online social networks but include social networking
features. To mention a few examples, Liben-Nowell et al. [49]
studied the LiveJournal online community and showed a
strong relationship between friendship and geography in social
networks. Cha et al. [50] presented a data-driven analysis of
user generated content video popularity distributions by using
data collected from YouTube and Daum. Gill et al. [51] also
studied a wide range of features of YouTube traffic, includ-
ing usage patterns, file properties, popularity and referencing
characteristics. In [36], we crawl Last.FM a music site with
social networking features.
C. Our prior and related work.
The conference version of this work appeared in [52].
This paper is revised and extended to include the following
materials. (i) A detailed discussion of the uniform userID
rejection sampling, which is used as ground truth in this
3
More specifically, it is most likely that for the collection of the social
graph, their BFS crawler does not follow users that have their “view profile”
privacy setting closed and “view friends“ privacy setting open.We infer that,
by the discrepancy in the percentage of users for those settings as reported in
a Facebook privacy study conducted during the same time in [46] i.e., in
networks New York, London, Australia, Turkey.
work; see Section III-D and Appendix A. (ii) An empirical
validation of the assumption that the social graph is static in
the time scales of the crawl; see Appendix B. (iii) A detailed
comparison of MHRW and RWRW methods and the finding
that RWRW is more efficient for all practical purposes; see
Section V-A for an experimental comparison on Facebook
and Appendix C for a comparison via analysis and simulation.
(iv) An extended section on the characterization of Facebook
based on a representative sample; see Section VI for additional
graphs on node properties and topological characteristics, and
new results on privacy settings. (iv) A comprehensive review
of related work in this section.
III. SAMPLING METHODOLOGY
We consider OSNs, whose social graph can be modeled as
a graph G = (V, E), where V is a set of nodes (users) and E
is a set of edges.
A. Assumptions
We make the following assumptions and discuss the extent
to which they hold:
A1 G is undirected. This is true in Facebook (its friendship
relations are mutual), but in Twitter the edges are directed,
which significantly changes the problem [20,29,53].
A2 We are interested only in the publicly available part of G.
This is not a big limitation in Facebook, because all the
information we collect is publicly available under default
privacy settings.
A3 G is well connected, and/or we can ignore isolated nodes.
This holds relatively well in Facebook thanks to its
high connection density. In contrast, in Last.fm the
friendship graph is highly fragmented, which may require
more sophisticated crawling approaches [36].
A4 G remains static during the duration of our crawl. We
argue in Appendix B that this assumption holds well in
Facebook.
A5 The OSN supports crawling. This means that on sampling
a node v we learn the identities of all its neighbors. It
is typically true in OSNs, e.g., through some mechanism
such as an API call or HTML scraping (both available in
Facebook).
B. Goal and applications
Our goal is to obtain a uniform sample (or more generally
a probability sample) of OSN users by crawling the social
graph. This is interesting in its own right, as it allows to
estimate frequencies of user attributes such as age, privacy
settings etc. Furthermore, a probability sample of users allows
us to estimate some local topological properties such as node
degree distribution, clustering and assortativity. In Section
VI-A, we compute the last two properties based on the one-
hop neighborhood of nodes. Therefore, a random sample of
nodes, obtained using our methodology, is a useful building
block towards characterizing structural properties.
We would like to emphasize, however, that a sample of
nodes cannot be directly used to obtain a “representative topol-
ogy” for estimating global structural properties. For example,
4

the nodes and edges in the sample, possibly together with their
neighbors (nodes and edges in the egonets) do not necessarily
provide a graph representative of the entire Facebook with
respect to properties such as e.g., geodesics. Therefore, if
global structural properties rather than local properties or
user attributes are of interest, our node sampling needs to be
combined with other techniques such as matrix completion
[54] or block modeling [55].
C. Sampling via crawling
The process of crawling the social graph starts with an
initially selected node and proceeds iteratively. In every op-
eration, we visit a node and discover all its neighbors. There
are many ways in which we can proceed, depending on which
neighbor we choose to visit next. In this section, we describe
the sampling methods implemented and compared in this
paper.
1) Breadth First Search (BFS): At each new iteration the
earliest explored but not-yet-visited node is selected next. As
this method discovers all nodes within some distance from the
starting point, an incomplete BFS is likely to densely cover
only some specific region of the graph.
2) Random Walk (RW): In the classic random walk [28],
the next-hop node w is chosen uniformly at random among
the neighbors of the current node v. I.e., the probability of
moving from v to w is
P
RW
v, w
=
1
k
v
if w is a neighbor of v,
0 otherwise.
RW is inherently biased. Assuming a connected graph and
aperiodicity, the probability of being at the particular node v
converges to the stationary distribution π
RW
v
=
k
v
2·|E|
, i.e. the
classic RW samples nodes w.p. π
RW
v
∼ k
v
. This is clearly
biased towards high degree nodes; e.g., a node with twice the
degree will be visited by RW twice more often. In Section V,
we show that several other node properties are correlated with
the node degree and thus estimated with bias by RW sampling.
3) Re-Weighted Random Walk (RWRW): A natural next step
is to crawl the network using RW, but to correct for the degree
bias by an appropriate re-weighting of the measured values.
This can be done using the Hansen-Hurwitz estimator
4
[56]
as first shown in [16,57] for random walks and also later used
in [17]. Consider a stationary random walk that has visited
V = v
1
, ...v
n
unique nodes. Each node can belong to one
of m groups with respect to a property of interest A, which
might be the degree, network size or any other discrete-valued
node property. Let (A
1
, A
2
, .., A
m
) be all possible values of
A and corresponding groups; ∪
m
1
A
i
= V . E.g., if the property
of interest is the node degree, A
i
contains all nodes u that
have degree k
u
= i. To estimate the probability distribution
of A, we need to estimate the proportion of nodes with value
4
The simple estimators we use in this paper, e.g., see Eq. (1), are Hansen-
Hurwitz estimators, which are well-known to have good properties (consistent
and unbiased) under mild conditions; see [55] for proof of consistency.
A
i
, i = 1, ..m:
ˆp(A
i
) =
P
u∈A
i
1/k
u
P
u∈V
1/k
u
(1)
Estimators for continuous properties can be obtained using
related methods, e.g., kernel density estimators.
4) Metropolis-Hastings Random Walk (MHRW): Instead of
correcting the bias after the walk, one can appropriately mod-
ify the transition probabilities so that the walk converges to
the desired uniform distribution. The Metropolis-Hastings al-
gorithm [58] is a general Markov Chain Monte Carlo (MCMC)
technique [59] for sampling from a probability distribution µ
that is difficult to sample from directly. In our case, we would
like to sample nodes from the uniform distribution µ
v
=
1
|V |
.
This can be achieved by the following transition probability:
P
MH
v, w
=
min(
1
k
v
,
1
k
w
) if w is a neighbor of v,
1 −
P
y6=v
P
MH
v, y
if w = v,
0 otherwise.
It can be shown that the resulting stationary distribution
is π
M H
v
=
1
|V |
, which is exactly the uniform distribution
we are looking for. P
MH
v, w
implies the following algorithm,
which we refer to simply as MHRW in the rest of the
paper:
v ← initial node.
while stopping criterion not met do
Select node w uniformly at random from neighbors of v.
Generate uniformly at random a number 0 ≤ p ≤ 1.
if p ≤
k
v
k
w
then
v ← w.
else
Stay at v
end if
end while
At every iteration of MHRW, at the current node v we
randomly select a neighbor w and move there w.p. min(1,
k
v
k
w
).
We always accept the move towards a node of smaller degree,
and reject some of the moves towards higher degree nodes.
This eliminates the bias towards high degree nodes.
D. Ground Truth: Uniform Sample of UserIDs (UNI)
Assessing the quality of any graph sampling method on an
unknown graph, as it is the case when measuring real systems,
is a challenging task. In order to have a “ground truth” to
compare against, the performance of such methods is typically
tested on artificial graphs.
Fortunately, Facebook was an exception during the time
period we performed our measurements. We capitalized on a
unique opportunity to obtain a uniform sample of Facebook
users by generating uniformly random 32-bit userIDs, and by
polling Facebook about their existence. If the userID exists
(i.e., belongs to a valid user), we keep it, otherwise we discard
it. This simple method is a textbook technique known as
rejection sampling [60] and in general it allows to sample from
any distribution of interest, which in our case is the uniform.
In particular, it guarantees to select uniformly random userIDs
from the allocated Facebook users regardless of their actual
5

distribution in the userID space, even when the userIDs are
not allocated sequentially or evenly across the userID space.
For completeness, we re-derive this property in Appendix VII.
We refer to this method as “UNI” and use it as a ground-truth
uniform sampler.
Although UNI sampling solves the problem of uniform node
sampling in Facebook, crawling remains important. Indeed,
the userID space must not be sparsely allocated for UNI to
be efficient. During our data collection (April-May 2009) the
number of Facebook users (∼ 200 × 10
6
) was comparable
to the size of the userID space (2
32
∼ 4.3 × 10
9
), resulting
in about one user retrieved per 22 attempts on average. If the
userID were 64 bit long or consisting of strings of arbitrary
length, UNI would had been infeasible.
5
In summary, we were fortunate to be able to obtain a
uniform independence sample of userIDs, which we then used
as a baseline for comparison (our “ground truth”) and showed
that our results conform closely to it. However, crawling
friendship relations is a fundamental primitive available in all
OSNs and, we believe, the right building block for designing
sampling techniques in OSNs in the general case.
E. Convergence
1) Using Multiple Parallel Walks: Multiple parallel walks
are used in the MCMC literature [59] to improve convergence.
Intuitively, if we only have one walk, the walk may get
trapped in cluster while exploring the graph, which may lead to
erroneous diagnosis of convergence. Having multiple parallel
walks reduces the probability of this happening and allows for
more accurate convergence diagnostics. An additional advan-
tage of multiple parallel walks, from an implementation point
of view, is that it is amenable to parallel implementation from
different machines or different threads in the same machine.
2) Detecting Convergence with Online Diagnostics: Valid
inferences from MCMC are based on the assumption that the
samples are derived from the equilibrium distribution, which
is true asymptotically. In order to correctly diagnose when
convergence to equilibrium occurs, we use standard diagnostic
tests developed within the MCMC literature [59]. In particular,
we would like to use diagnostic tests to answer at least the
following questions:
• How many of the initial samples in each walk do we need
to discard to lose dependence from the starting point (or
burn-in) ?
• How many samples do we need before we have collected
a representative sample?
A standard approach is to run the sampling long enough
and to discard a number of initial burn-in samples proactively.
From a practical point of view, however, the burn-in comes at a
cost. In the case of Facebook, it is the consumed bandwidth
(in the order of gigabytes) and measurement time (days or
5
To mention a few such cases in the same time frame: Orkut had a 64bit
userID and hi5 used a concatenation of userID+Name. Interestingly, within
days to weeks after our measurements were completed, Facebook changed
its userID allocation space from 32 bit to 64 bit [61]. Section V-B3 contains
more information about userID space usage in Facebook in April 2009.
Fig. 1. Basic node information collected when visiting a user u.
weeks). It is therefore crucial to assess the convergence of
our MCMC sampling, and to decide on appropriate settings
of burn-in and total running time.
Given that during a crawl we do not know the target
distribution, we can only estimate convergence from the sta-
tistical properties of the walks as they are collected. Here
we present two standard convergence tests, widely accepted
and well documented in the MCMC literature, Geweke [62]
and Gelman-Rubin [63], described below. In Section V, we
apply these tests on several node properties, including the
node degree, userID, network ID and membership in a specific
network; please see Section V-A5 for details. Below, we briefly
outline the rationale of these tests.
Geweke Diagnostic. The Geweke diagnostic [62] detects
the convergence of a single Markov chain. Let X be a
single sequence of samples of our metric of interest. Geweke
considers two subsequences of X, its beginning X
a
(typically
the first 10%), and its end X
b
(typically the last 50%). Based
on X
a
and X
b
, we compute the z-statistic:
z =
E(X
a
) − E(X
b
)
p
V ar(X
a
) + V ar(X
b
)
With increasing number of iterations, X
a
and X
b
move further
apart, which limits the correlation between them. As they
measure the same metric, they should be identically distributed
when converged and, according to the law of large numbers,
the z values become normally distributed with mean 0 and
variance 1. We can declare convergence when all values fall
in the [−1, 1] interval.
Gelman-Rubin Diagnostic. Monitoring one long sequence
of nodes has some disadvantages. For example, if our chain
stays long enough in some non-representative region of the
parameter space, we might erroneously declare convergence.
For this reason, Gelman and Rubin [63] proposed to monitor
m > 1 sequences. Intuitively speaking, the Gelman-Rubin
diagnostic compares the empirical distributions of individ-
ual chains with the empirical distribution of all sequences
together: if these two are similar, we declare convergence.
The test outputs a single value R that is a function of means
and variances of all chains. With time, R approaches 1, and
convergence is declared typically for values smaller than 1.02.
6
bit attribute explanation
1 Add as friend =1 if w can propose to ‘friend’ u
2
Photo =1 if w can see the profile photo of u
3 View friends =1 if w can see the friends of u
4 Send message =1 if w can send a message to u
TABLE I
PRIVACY SETTINGS OF A USER u WITH RESPECT TO HER NON-FRIEND w.
IV. DATA COLLECTION
A. User properties of interest
Fig. 1 summarizes the information collected when visiting
the “show friends” web page of a sampled user u, which we
refer to as basic node information.
Name and userID. Each user is uniquely defined by her
userID, which is a 32-bit number
6
. Each user presumably
provides her real name. The names do not have to be unique.
Friends list. A core idea in social networks is the possibility
to declare friendship between users. In Facebook, friendship
is always mutual and must be accepted by both sides. Thus
the social network is undirected.
Networks. Facebook uses two types of “networks” to
organize its users. The first are regional (geographical) net-
works
7
. There are 507 predefined regional networks that
correspond to cities, regions, and countries around the world.
A user can freely join any regional network but can be a
member of only one regional network at a time. Changes
are allowed, but no more than twice every 6 months (April
2009). The second type of networks contain user affiliations
with colleges, workplaces, and high schools and have stricter
membership criteria: they require a valid email account from
the corresponding domain, e.g., to join the UC Irvine network
you have to provide a “@uci.edu” email account. A user can
belong to many networks of the second type.
Privacy settings Q
v
. Each user u can restrict the amount
of information revealed to any non-friend node w, as well as
the possibility of interaction with w. These are captured by
four basic binary privacy attributes, as described in Table I.
We refer to the resulting 4-bit number as privacy settings Q
v
of node v. By default, Facebook sets Q
v
= 1111 (allow all).
Friends of u. The “show friends” web page of user u
exposes network membership information and privacy settings
for each listed friend. Therefore, we collect such information
for all friends of u, at no additional cost.
Profiles. Much more information about a user can poten-
tially be obtained by viewing her profile. Unless restricted by
the user, the profile can be displayed by her friends and users
from the same network. In this work, we do not collect any
profile information, even if it is publicly available. We study
only the basic node information shown in Fig.1.
6
Facebook changed to 64-bit user ID space after May 2009 [61] whereas
our crawls were collected during April-May 2009.
7
Regional networks were available at the time of this study but were phased
out starting from June 2009 [64]
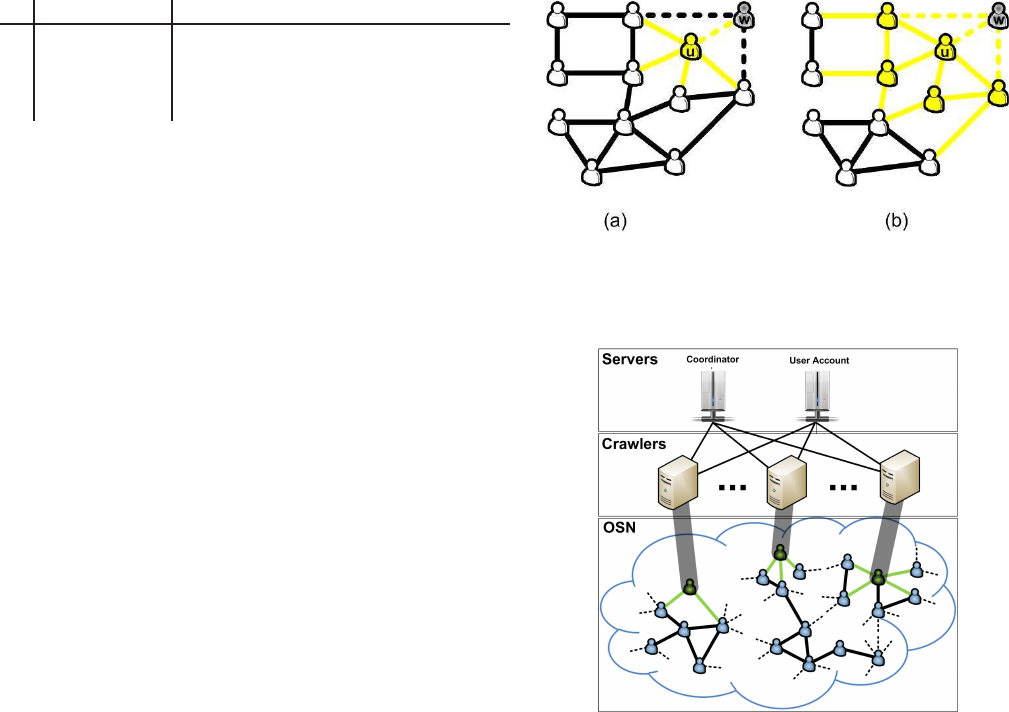
Fig. 2. (a) Sampled user u with observed edges in yellow color. (b) The
extended ego network of user u with observed nodes and edges in yellow
color. Invalid neighbor w, whose privacy settings Q
w
= ∗ ∗ 0∗ do not allow
friend listing, is discarded.
Fig. 3. Distributed Crawling of an Online Social Network
Ego Networks. The sample of nodes collected by our
method enables us to study many features of FB users in a
statistically unbiased manner. However, more elaborate topo-
logical measures, such as clustering coefficient and assortativ-
ity, cannot be easily estimated based purely on a single-node
view. For this reason, we decided to also collect a number
of extended ego nets
8
(see Fig 2), for ∼37K “ego” nodes,
randomly selected from all nodes in MHRW.
B. Crawling Process
In order to apply our methodology to real-life OSNs,
we implemented high-performance distributed crawlers that
explored the social graph in a systematic and efficient way.
1) Challenges: There are several practical challenges we
faced while crawling the social graph of OSNs. First, OSNs
usually use some defense mechanisms against automated
data mining. Mislove et al. [12] reported rate limits per IP
8
We use the extended egonet sample differently from the Random Node
Neighbor (RNN) sample presented in [32]. We are interested in estimating
properties of the ego nodes only whereas RNN [32] looks at the induced
subgraph of all sampled nodes and is interested in estimating properties of
the ego and all alters. Therefore, the sample of extended egonets, that we
collect in this work, is expected to capture very well community structure
properties (i.e., clustering coefficient) of the whole Facebook population.
7

Crawling method MHRW RW BFS UNI
Total number of valid users 28×81K 28×81K 28×81K 984K
Total number of unique users 957K 2.19M 2.20M 984K
Total number of unique neighbors
72.2M 120.1M 96M 58.4M
Crawling period 04/18-04/23 05/03-05/08 04/30-05/03 04/22-04/30
Avg Degree 95.2 338 323 94.1
Median Degree 40 234 208 38
Number of overlapping users
MHRW ∩ RW 16.2K
MHRW ∩ BFS 15.1K
MHRW ∩ Uniform 4.1K
RW ∩ BFS 64.2K
RW ∩ Uniform 9.3K
BFS ∩ Uniform 15.1K
TABLE II
(LEFT:) DATASETS COLLECTED BY MHRW, RW, BFS AND UNI IN 2009. (RIGHT:)THE OVERLAP BETWEEN DIFFERENT DATASETS IS SMALL.
while crawling Orkut. Similarly, in our Facebook crawls
we experienced banned accounts, probably due to excessive
traffic. Second, in Facebook, the API calls are usually more
restrictive than HTML scraping, which forced us to implement
the latter. Third, many modern web sites enable asynchronous
loading of web content (i.e., use AJAX), which requires more
sophisticated customization of the crawlers. Finally, in order
to satisfy assumption A4, the data collection time should be
relatively small, in the order of a few days (see Appendix B).
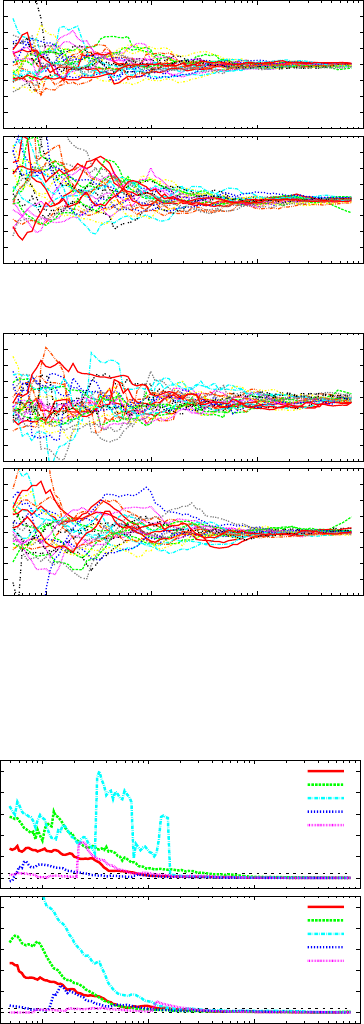
2) Implementation: Fig 3 depicts an overview of our dis-
tributed crawling process.
First, we use a large number of machines with limited
memory (100 Mbytes-1GBytes RAM) and disk space (up to
5GBytes), to parallelize our crawling and shorten the data
collection time. We have up to three layers of parallelism
in each machine. Each crawling machine runs one or more
crawling processes. Each crawling process shares one user
account between multiple crawling threads within it. Each
crawling thread fetches data asynchronously where possible.
Second, we use one machine as coordinator server that
(i) controls the number of connections or amount of bandwidth
over the whole cluster, (ii) keeps track of already fetched users
to avoid fetching duplicate data, and (iii) maintains a data
structure that stores the crawl frontier, e.g., a queue for BFS.
Third, a user account server stores the login/API accounts,
created manually by the administrator. When a crawling pro-
cess is initiated, it requests an unused account from the user
account server; the crawling process is activated only if a valid
account is available.
3) Invalid users: There are two types of users that we
declare as invalid. First, if a user u decides to hide her friends
and to set the privacy settings to Q
u
= ∗∗0∗, the crawl cannot
continue. We address this problem by backtracking to the
previous node and continuing the crawl from there, as if u was
never selected. Second, there exist nodes with degree k
v
= 0;
these are not reachable by any crawls, but we stumble upon
them during the UNI sampling of the userID space. Discarding
both types of nodes is consistent with our assumptions (A2,
A3), where we already declared that we exclude such nodes
(either not publicly available (A2) or isolated (A3)) from the
graph we want to sample.
4) Execution of crawls: We ran 28 different independent
crawls for each crawling methodology, namely MHRW, BFS
and RW, all seeded at the same set of randomly selected nodes.
We collected exactly 81K samples for each independent crawl.
We count towards this value all repetitions, such as the self-
transitions of MHRW, and returning to an already visited state
(RW and MHRW). In addition to the 28×3 crawls (BFS, RW
and MHRW), we ran the UNI sampling until we collected
984K valid users, which is comparable to the 957K unique
users collected with MHRW.
C. Description of Datasets
Table II summarizes the datasets collected using the crawl-
ing techniques under comparison. This information refers to
all sampled nodes, before discarding any burn-in. For each of
MHRW, RW, and BFS, we collected the total of 28 × 81K =
2.26M nodes. However, because MHRW and RW sample with
repetitions, and because the 28 BFSes may partially overlap,
the number of unique nodes sampled by these methods is
smaller. This effect is especially visible under MHRW that
collected only 957K unique nodes. Table II(right) shows that
the percentage of common users between the MHRW, RW,
BFS and UNI datasets is very small, as expected. The largest
observed, but still objectively small, overlap is between RW
and BFS and is probably due to the common starting points
selected.
To collect the UNI dataset, we checked ∼ 18.5M user
IDs picked uniformly at random from [1, 2
32
]. Out of them,
only 1,216K users existed. Among them, 228K users had zero
friends; we discarded these isolated users to be consistent with
our problem statement. This results in a set of 984K valid users
with at least one friend each.
To analyze topological characteristics of the Facebook
population, we collected ∼ 37K egonets that contain basic
node information (see Fig 1) for ∼ 5.8M unique neighbors.
Table III contains a summary of the egonet dataset, including
properties that we analyze in section VI.
Number of egonets 37K
Number of neighbors 9.3M
Number of unique neighbors 5.8M
Crawling period
04/24-05/01
Avg Clustering coefficient 0.16
Avg Assortativity 0.233
TABLE III
EGO NETWORKS COLLECTED FOR 37K NODES, RANDOMLY SELECTED
FROM THE USERS IN THE MHRW DATASET.
Overall, we sampled 11.6 million unique nodes, and ob-
served other 160M as their (unsampled) neighbors. This is a
very large sample by itself, especially given that Facebook
8
had reported having close to 200 million active users during
the time of these measurements.
V. EVALUATION OF SAMPLING TECHNIQUES
In this section, we evaluate all candidate crawling tech-
niques (namely BFS, RW and RWRW, MHRW), in terms of
their efficiency (convergence) and quality (estimation bias). In
Section V-A, we study the convergence of the random walk
methods with respect to several properties of interest. We find
a burn-in period of 6K samples, which we exclude from each
independent crawl. The remaining 75K x 28 sampled nodes
is our main sample dataset; for a fair comparison we also
exclude the same number of burn-in samples from all datasets.
In Section V-B we examine the quality of the estimation based
on each sample. In Section V-C, we summarize our findings
and provide practical recommendations.
A. Convergence analysis
There are several crucial parameters that affect the conver-
gence of a Markov Chain sample. In this section, we study
these parameters by (i) applying formal convergence tests and
(ii) using simple, yet insightful, visual inspection of the related
traces and histograms.
1) Burn-in: For the random walk-based methods, a number
of samples need to be discarded to lose dependence on the
initial seed point. Since there is a cost for every user we
sample, we would like to choose this value using formal
convergence diagnostics so as not to waste resources. Here, we
apply the convergence diagnostics presented in Section III-E2
to several properties of the sampled nodes and choose as burn-
in the maximum period from all tests.
The Geweke diagnostic is applied in each of the 28 walks
separately and compares the difference between the first 10%
and the last 50% of the walk samples. It declares convergence
when all 28 values fall in the [−1, 1] interval. Fig. 4 presents
the results of the Geweke diagnostic for the user properties
of node degree and regional network membership. We start at
50 iterations and plot 150 points logarithmically spaced. We
observe that after approximately 500−2000 iterations we have
a z-score strictly between [−1, 1]. We also see that RWRW and
MHRW perform similarly w.r.t. the Geweke diagnostic.
The Gelman-Rubin diagnostic analyzes all the 28 walks
at once by summarizing the difference of the between-walk
variances and within-walk variances. In Fig. 5 we plot the
R score for the following metrics (i) number of friends (or
node degree) (ii) networkID (or regional network) (iii) privacy
settings Q
v
(iv) membership in specific regional networks,
namely Australia, New York and Colombia. The last user
property is defined as follows: if the user in iteration i is a
member of network x then the metric is set to 1, otherwise it
is set to 0. We can see that the R score varies considerably in
the initial hundred to thousand iterations for all properties. To
pick an example, we observe a spike between iterations 1, 000
and 2, 000 in the MHRW crawl for the New York membership.
This is most likely the result of certain walks getting trapped
within the New York network, which is particularly large.
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Geweke Z-Score
RWRW
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
100 1000 10000 100000
Geweke Z-Score
Iterations
MHRW
(a) Number of friends
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Geweke Z-Score
RWRW
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
100 1000 10000 100000
Geweke Z-Score
Iterations
MHRW
(b) Regional network ID
Fig. 4. Geweke z score (0K..81K) for number of friends (top) and regional
network affiliation (bottom). Each line shows the Geweke score for each of
the 28 parallel walks.
1
1.1
1.2
1.3
1.4
1.5
R value
RWRW
Number of friends
Regional Network ID
Privacy
Australia Membership in (0,1)
New York Membership in (0,1)
1
1.1
1.2
1.3
1.4
1.5
100 1000 10000 100000
R value
Iterations
MHRW
Number of friends
Regional Network ID
Privacy
Australia Membership in (0,1)
New York Membership in (0,1)
Fig. 5. Gelman-Rubin R score (0K..81K) for five different metrics.
Eventually, after 3000 iterations all the R scores for the
properties of interest drop below 1.02, the typical target value
used for convergence indicator.
We declare convergence when all tests have detected it.
The Gelman-Rubin test is the last one at 3K nodes. To be
even safer, in each independent walk we conservatively discard
6K nodes, out of 81K nodes total. In the remainder of the
evaluation, we work only with the remaining 75K nodes per
9

-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Geweke Z-Score
RWRW
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
100 1000 10000 100000
Geweke Z-Score
Iterations
MHRW
(a) Geweke on Number of Friends
1
1.1
1.2
1.3
1.4
1.5
R value
RWRW
Number of friends
Regional Network ID
Privacy
Australia Membership in (0,1)
New York Membership in (0,1)
1
1.1
1.2
1.3
1.4
1.5
100 1000 10000 100000
R value
Iterations
MHRW
Number of friends
Regional Network ID
Privacy
Australia Membership in (0,1)
New York Membership in (0,1)
(b) Gelman Rubin
Fig. 6. Online convergence diagnostics for samples 6K..81K (without burn-
in). (top) Geweke z score for number of friends. (bottom) Gelman-Rubin score
for five different metrics.
independent chain for RW, RWRW and MHRW.
2) Total Running Time: Another decision we have to make
is about the walk length, excluding the burn-in samples. This
length should be appropriately long to ensure that we are
at equilibrium. Here, we utilize multiple ways to analyze
the collected samples, so as to increase our confidence that
the collected samples are appropriate for further statistical
analysis.
First, we apply formal convergence diagnostics that allow
us to assess convergence online by indicating approximate
equilibrium. Fig 6 shows the Geweke z-score for the number of
friends (top) and the Gelman-Rubin R score for five different
properties (bottom). These results are obtained after discarding
the burn-in samples (0K..6K). They show that convergence
is attained with at least 3k samples per walk, similar to
the section in which we determined the burn-in. This is an
indication that the Facebook social graph is well connected
and our random walks achieved good mixing with our initial
selection of random seeds.
Second, we perform visual inspection to check the con-
vergence state of our sample by plotting for each walk the
running mean of a user property against the iteration number.
The intuition is that if convergence has been reached, the
running mean of the property will not drastically change as
P(k
v
= k) P(k
v
= k) P(k
v
= k)
Fig. 8. The effect of walk length and thinning on the results. We present
histograms of visits at nodes with a specific degree k ∈ {10, 50, 100, 200}
and network membership (Australia, New York, India, Vancouver), generated
under three conditions. (top): All nodes visited after the first 6K burn-in nodes.
(middle): 5K consecutive nodes, from hop 50K to hop 55K. This represents a
short walk length. (bottom): 5k nodes by taking every 10th sample (thinning).
the number of iterations increases. Fig 7 shows for each crawl
type the running mean (i) for the node degree in the UNI
sample, (ii) in each of the 28 walks individually, and (iii) in
an average crawl that combines all 28 walks. It can be seen
that in order to estimate the average node degree
k
v
based on
only a single MHRW or RW walk, we should take at least
10K iterations to be likely to get within ±10% off the real
value. In contrast, averaging over all 28 walks seems to provide
similar or better confidence after fewer than 100 iterations per
walk or 100 × 28 ∼ 3k samples over all walks. Additionally,
the average MHRW and RW crawls reach stability within
350 × 28 ∼ 10K iterations. It is quite clear that the use of
multiple parallel walks is very beneficial in the estimation of
user properties of interest.
According to the diagnostics and visual inspection, we need
at least 3k samples per walk or 3k × 28 ∼ 84k over all walks.
Since we were not resource constrained during our crawling,
we continued sampling users until we reached 81K per walk.
One obvious reason is that more samples should decrease the
estimation variance. Another reason is that more samples allow
us to break the correlation between consecutive samples by
thinning the set of sampled users. We use such a thinning
process to collect egonets.
3) Thinning: Let us examine the effect of a larger sample
on the estimation of user properties. Fig. 8 shows the percent-
age of sampled users with specific node degrees and network
affiliations, rather than the average over the entire distribution.
A walk length of 75K (top) results in much smaller estimation
variance per walk than taking 5K consecutive iterations from
50-55k (middle). Fig.8 also reveals the correlation between
consecutive samples, even after equilibrium has been reached.
It is sometimes reasonable to break this correlation, by con-
sidering every ith sample, a process which is called thinning.
The bottom plots in Fig. 8 show 5K iterations per walk with
a thinning factor of i = 10. It performs much better than the
middle plot, despite the same total number of samples.
10

k
v
Iterations
(a) MHRW
k
v
Iterations
(b) RWRW
k
v
Iterations
(c) RW
k
v
Iterations
(d) BFS
Fig. 7. Average node degree
k
v
observed by each crawl, as a function of the number of iterations (or running mean).
RWRW
RWRW-Uniq
MHRW
MHRW-Uniq
Fig. 9. The efficiency of RWRW and MHRW in estimating the degree
distribution of Facebook, in terms of the Kullback-Leibler (KL) divergence.
The “Uniq” plots count as iterations only the number of unique sampled nodes,
which represents the real bandwidth cost of sampling.
Thinning in MCMC samplings has the side advantage of
saving space instead of storing all collected samples. In the
case of crawling OSNs, the main bottleneck is the time and
bandwidth necessary to perform a single transition, rather
than storage and post-processing of the extracted information.
Therefore we did not apply thinning to our basic crawls.
However, we applied another idea (sub-sampling), that has
a similar effect with thinning, when collecting the second
part of our data - the egonets. Indeed, in order to collect
the information on a single egonet, our crawler had to visit
the user and all its friends, an average ∼ 100 nodes. Due
to bandwidth and time constraints, we could fetch only 37K
egonets. In order to avoid correlations between consecutive
egonets, we collected a random sub-sample of the MHRW
(post burn-in) sample, which essentially introduced spacing
among sub-sampled nodes.
4) Comparison to Ground Truth: Finally, we compare the
random walk techniques in terms of their distance from the
true uniform (UNI) distribution as a function of the iterations.
In Fig. 9, we show the distance of the estimated distribution
from the ground truth in terms of the KL (Kullback-Leibler)
metric, that captures the distance of the 2 distributions ac-
counting for the bulk of the distributions. We also calculated
the Kolmogorov-Smirnov (KS) statistic, not shown here, which
captures the maximum vertical distance of two distributions.
We found that RWRW is more efficient than MHRW with
respect to both statistics. We note that the usage of distance
metrics such as KL and KS cannot replace the role of the
formal diagnostics which are able to determine convergence
online and most importantly in the absence of the ground truth.
5) The choice of metric matters: MCMC is typically used
to estimate some user property/metric, i.e., a function of the
underlying random variable. The choice of metric can greatly
affect the convergence time. We chose the metrics in the
diagnostics, guided by the following principles:
• We chose the node degree because it is one of the metrics
we want to estimate; therefore we need to ensure that the
MCMC has converged at least with respect to it. The
distribution of the node degree is also typically heavy
tailed, and thus is slow to converge.
• We also used several additional metrics (e.g. network ID,
user ID and membership to specific networks), which are
uncorrelated to the node degree and to each other, and
thus provide additional assurance for convergence.
• We essentially chose to use all the nodal attributes that
were easily and cheaply accessible at each node. These
metrics were also relevant to the estimation at later
sections.
Let us focus on two of these metrics of interest, namely
node degree and sizes of geographical network and study their
convergence in more detail. The results for both metrics and all
three methods are shown in Fig.10. We expected node degrees
to not depend strongly on geography, while the relative size
of geographical networks to strongly depend on geography.
This implies that (i) the degree distribution will converge fast
to a good uniform sample even if the walk has poor mixing
and stays in the same region for a long time; (ii) a walk that
mixes poorly will take long time to barely reach the networks
of interest, not to mention producing a reliable network size
estimate. In the latter case, MHRW will need a large number
of iterations before collecting a representative sample.
The results presented in Fig. 10 (bottom) confirm our
expectation. MHRW performs much better when estimating
the probability of a node having a given degree, than the
probability of a node belonging to a specific regional network.
For example, one MHRW crawl overestimates the size of
“New York, NY” by roughly 100%. The probability that a
perfect uniform sampling makes such an error (or larger) is
P
∞
i=i
0
i
n
p
i
(1 − p)
i
≃ 4.3 · 10
−13
, where we took i
0
= 1k,
n = 81K and p = 0.006. Even given such single-walk
deviations, the multiple-walk average for the MHRW crawl
provides an excellent estimate of the true population size.
B. Unbiased Estimation
This section presents the main results of this chapter. First,
the MHRW and RWRW methods perform very well: they
estimate two distributions of interest (namely node degree,
11

P(k
v
= k) P(k
v
= k) P(k
v
= k) P(k
v
= k)
node degree k
P(N
v
= N ) P(N
v
= N ) P(N
v
= N ) P(N
v
= N )
regional network N
Fig. 10. Histograms of visits at node of a specific degree (left) and in a specific regional network (right). We consider four sampling techniques: BFS, RW,
RWRW and MHRW. We present how often a specific type of node is visited by the 28 crawlers (‘crawls’), and by the uniform UNI sampler (‘uniform’). We
also plot the visit frequency averaged over all the 28 crawlers (‘average crawl’). Finally, ‘size’ represents the real size of each regional network normalized
by the the total Facebook size. We used all the 81K nodes visited by each crawl, except the first 6K burn-in nodes. The metrics of interest cover roughly
the same number of nodes (about 0.1% to 1%), which allows for a fair comparison.
P(k
v
= k)
P(k
v
= k)
P(k
v
= k)
P(k
v
= k)
node degree knode degree k
node degree knode degree k
Fig. 11. Degree distribution (pdf) estimated by the sampling techniques
and the ground truth (uniform sampler). MHRW and RWRW agree almost
perfectly with the UNI sample; while BFS and RW deviate significantly. We
use log-log scale and logarithmic binning of data in all plots.
regional network size) essentially identically to the UNI sam-
pler. Second, the baseline algorithms (BFS and RW) deviate
substantively from the truth and lead to misleading estimates.
1) Node degree distribution: In Fig. 11 we present the
degree distributions estimated by MHRW, RWRW, RW, and
BFS. The average MHRW crawl’s pdf, shown in Fig. 11(a) is
virtually identical to UNI. Moreover, the degree distribution
found by each of the 28 chains separately are almost identical.
In contrast, RW and BFS shown in Fig. 11(c) and (d) introduce
a strong bias towards the high degree nodes. For example,
the low-degree nodes are under-represented by two orders of
magnitude. As a result, the estimated average node degree
is
k
v
≃ 95 for MHRW and UNI, and k
v
≃ 330 for BFS
and RW. Interestingly, this bias is almost the same in the
case of BFS and RW, but BFS is characterized by a much
higher variance. Notice that that BFS and RW estimate wrong
not only the parameters but also the shape of the degree
distribution, thus leading to wrong information. Re-weighting
the simple RW corrects for the bias and results to RWRW,
which performs almost identical to UNI, as shown in 11(b).
As a side observation we can also see that the true degree
distribution clearly does not follow a power-law.
2) Regional networks: Let us now consider a geography-
dependent sensitive metric, i.e., the relative size of regional
networks. The results are presented in Fig. 10 (right). BFS
performs very poorly, which is expected due to its local
coverage. RW also produces biased results, possibly because of
a slight positive correlation that we observed between network
size and average node degree. In contrast, MHRW and RWRW
perform very well albeit with higher variance, as already
discussed in Section V-A5.
12

degree k
v
userID
userID
cdf
Fig. 12. User ID space usage discovered by BFS, RW, MHRW and UNI.
Each user is assigned a 32 bit long userID. Although this results in numbers
up to 4.3e9, the values above 1.8e9 almost never occur. Inset: The average
node degree (in log scale) as a function of userID.
3) The userID space: Finally, we look at the distribution of
a property that is completely uncorrelated from the topology
of Facebook, namely the user ID. When a new user joins
Facebook, it is automatically assigned a 32-bit number,
called userID. It happens before the user specifies its profile,
joins networks or adds friends, and therefore one could expect
no correlations between userID and these features. In other
words, the degree bias of BFS and RW should not affect the
usage of userID space. Therefore, at first, we were surprised
to find big differences in the usage of userID space discovered
by BFS, RW and MHRW. We present the results in Fig 12.
Note that the userID space is not covered uniformly, prob-
ably for historical reasons. BFS and RW are clearly shifted
towards lower userIDs. The origin of this shift is probably
historical. The sharp steps at 2
29
≃0.5e9 and at 2
30
≃1.0e9
suggest that Facebook was first using only 29 bit of userIDs,
then 30, and now 31. As a result, users that joined earlier have
the smaller userIDs. At the same time, older users should have
higher degrees on average, which implies that userIDs should
be negatively correlated with node degrees. This is indeed the
case, as we show in the inset of Fig 12.
9
This, together with
the degree bias of BFS and RW, explains the shifts of userIDs
distributions observed in the main plot in Fig 12. In contrast to
BFS and RW, MHRW performed extremely well with respect
to the userID metric.
C. Findings and Practical Recommendations
1) Choosing between methods: First and most important,
the above comparison demonstrates that both MHRW and
RWRW succeed in estimating several Facebook properties
of interest virtually identically to UNI. In contrast, commonly
used baseline methods (BFS and simple RW) fail, i.e., deviate
9
Our observations are also confirmed by internal sources within Facebook
[65]. According to them, Facebook’s user ID assignment reflects the history
of the website and has transitioned through several phases. Initially, userIDs
were auto-incremented starting at 4. As more networks, such as colleges or
high schools, were supported, customized userID spaces were assigned per
college i.e., Stanford IDs were assigned between 200000-299999. Finally,
open registration to all users introduced scalability problems and made userID
assignment less predictable.
significantly from the truth and lead to substantively erroneous
estimates. Moreover, the bias of BFS and RW shows up
not only when estimating directly node degrees (which was
expected), but also when we consider other metrics seemingly
uncorrelated metrics (such as the size of regional network),
which end up being correlated to node degree. This makes
the case for moving from “1st generation” traversal methods
such as BFS, which have been predominantly used in the
measurements community so far [9,12,13], to more principled,
“2nd generation”, sampling techniques whose bias can be
analyzed and/or corrected for. The random walks considered
in this paper, RW, RWRW and MHRW, are well-known in
the field of Monte Carlo Markov Chains (MCMC). We apply
and adapt these methods to Facebook, for the first time, and
we demonstrate that, when appropriately used, they perform
remarkably well on real-world OSNs.
2) Adding convergence diagnostics and parallel crawls:
A key ingredient of our implementation - to the best of our
knowledge, not previously employed in network sampling -
was the use of formal online convergence diagnostic tests.
We tested these on several metrics of interest within and
across chains, showing that convergence was obtained within
a reasonable number of iterations. We believe that such tests
can and should be used in field implementations of walk-
based sampling methods to ensure that samples are adequate
for subsequent analysis. Another key ingredient of our imple-
mentation was the use of independent crawlers (started from
several random independent starting points, unlike [17,19] who
use a single starting point), which both improved convergence
and decreased the duration of the crawls.
3) MHRW vs. RWRW: Both MHRW and RWRW achieved
a uniform sample. When comparing the two, RWRW is
slightly more efficient, i.e., needed less samples for the same
accuracy. This is consistent with the findings in [17,19]. This
is partly due to the fact that MHRW requires a large number of
rejections during the initial sampling process; and partly due
to slower mixing, in practice, as it avoids high degree nodes.
In this section, we present an empirical comparison based on
the Facebook experiments. In Appendix C, we provide a
more in-depth comparison via analysis and simulation.
However, when choosing between the two methods there
are additional trade-offs to consider. First, MHRW yields
an asymptotically uniform sample, which requires no addi-
tional processing for subsequent analysis. By contrast, RWRW
samples are heavily biased towards high-degree nodes, and
require use of appropriate re-weighting procedures to generate
correct results. For the creation of large data sets intended for
general distribution (as in the case of our Facebook sample),
this “ready-to-use” aspect of MHRW has obvious merit
10
. A
second advantage of MHRW is the ease of online testing for
convergence to the desired target (uniform) distribution. In
contrast, in RWRW, we test for convergence on a different dis-
10
For example, our released data sets [21] are intended to be used by people
that are not necessarily experts in the re-weighting methods, for whom the
potential for erroneous misuse is high
13

tribution and then re-weight, which can introduce distortion
11
.
Finally, simple re-weighting is difficult or impossible to apply
in the context of many purely data-analytic procedures such as
multidimensional scaling or hierarchical clustering. Simulated
Importance Resampling [66] provides a useful alternative for
RWRW samples, but suffers from well-known problems of
asymptotic bias (see [67] for a discussion). This is of less
concern for applications such as moment estimation, for which
re-weighting is both simple and effective.
Ultimately, the choice of RWRW versus MHRW is thus
a trade-off between efficiency during the initial sampling
process (which favors RWRW in all practical cases) and
simplicity/versatility of use for the resulting data set (which
favors MHRW). For our present purposes, these trade-offs
favor MHRW, and we employ it here for producing a uniform
ready-to-use sample of users.
VI. FACEBOOK CHARACTERIZATION
In this section, we use the uniform sample of 1M nodes, col-
lected through MHRW, and the sub-sample of 37K extended
egonets to study some features of Facebook. In contrast to
previous work, which focused on particular regions [11,45] or
used larger but potentially biased samples [12,13], our user
sample is representative of the entire Facebook.
A. Topological Characteristics
We first focus on purely topological aspects of the graph of
Facebook.
1) Degree distribution: Node degree is just one example
of a node-level (user) property, which also happens to be
an important topological characteristic In Fig. 11(a,b), we
present the node degree distribution of Facebook. Differ-
ently from previous studies of crawled datasets in online social
networks in [9,12,13], we observe that node degree is not
a power law. Instead, we can identify two regimes, roughly
1 ≤ k < 300 and 300 ≤ k ≤ 5000, each of which can be
approximated by a power-law with exponents α
k<300
= 1.32
and α
k≥300
= 3.38, respectively. We note, however, that the
regime 300 ≤ k ≤ 5000 covers only slightly more than one
decade. This behavior is suggestive of multistage “vetting”
models of network formation.
2) Assortativity: Depending on the type of complex net-
work, nodes may tend to connect to similar or different nodes.
For example, in many social networks high degree nodes tend
to connect to other high degree nodes [68]. Such networks are
called assortative. In Fig.13, we plot the node degree vs. the
degrees of its neighbors. We observe a positive correlation,
which implies assortative mixing and is in agreement with
previous studies of similar social networks. We can also
summarize this plot by calculating the Pearson correlation
coefficient, or assortativity coefficient which is r = 0.233.
This value is higher than r
′
= 0.17 reported in [13]. A
11
It is in principle possible to diagnose convergence on re-weighted
statistics with RWRW. However, this requires appropriate use of re-weighting
during the convergence evaluation process, which can increase the complexity
of implementation.
neighbor node degree k
′
node degree k
Fig. 13. Assortativity - correlation between degrees of neighboring nodes.
The dots represent the degree-degree pairs (randomly subsampled for visual-
ization only). The line uses log-binning and takes the average degree of all
nodes that fall in a corresponding bin.
clustering coefficient C(k)
node degree k
Fig. 14. Clustering coefficient of Facebook users as function of their
degree.
possible explanation is that the Region-Constrained BFS used
in [13] stops at regional network boundaries and thus misses
many connections to, typically high-degree, nodes outside the
network.
3) Clustering coefficient: In social networks, it is likely
that two friends of a user are also friends of each other. The
intensity of this phenomenon can be captured by the clustering
coefficient C
v
of a node v, defined as the relative number of
connections between the nearest neighbors of v. The clustering
coefficient of a network is the average C over all nodes. We
find the average clustering coefficient of Facebook to be
C = 0.16, similar to that reported in [13]. Since the clustering
coefficient tends to depend strongly on the node’s degree k
v
,
we looked at C
v
as a function of k
v
. Fig. 14 shows a larger
range in the degree-dependent clustering coefficient ([0.05,
0.35]) than what was found in [13] ([0.05, 0.18]).
P(Q
v
)
privacy settings Q
v
Fig. 15. The distribution of the privacy settings among ∼ 172M Facebook
users. Value Q
v
=1111 corresponds to default settings (privacy not restricted)
and covers 84% of all users.
14

P A Network n P A Network n
0.08 Iceland ... .. .
0.11 Denmark 0.22 Bangladesh
0.11 Provo, UT 0.23 Hamilton, ON
0.11 Ogden, UT 0.23 Calgary, AB
0.11 Slovakia 0.23 Iran
0.11 Plymouth 0.23 India
0.11 Eastern Idaho, ID 0.23 Egypt
0.11 Indonesia 0.24 United Arab Emirates
0.11 Western Colorado, CO 0.24 Palestine
0.11 Quebec City, QC 0.25 Vancouver, BC
0.11 Salt Lake City, UT 0.26 Lebanon
0.12 Northern Colorado, CO 0.27 Turkey
0.12 Lancaster, PA 0.27 Toronto, ON
0.12 Boise, ID 0.28 Kuwait
0.12 Portsmouth 0.29 Jordan
... .. . 0.30 Saudi Arabia
TABLE IV
REGIONAL NETWORKS WITH RESPECT TO THEIR PRIVACY AWARENESS
P A = P(Q
v
6=1111 |v ∈ n) AMONG ∼ 172M Facebook USERS. ONLY
REGIONS WITH AT LEAST 50K USERS ARE CONSIDERED. NOTE THE
DIFFERENT TYPES OF COUNTRIES IN THE TWO EXTREME ENDS OF THE
SPECTRUM. E.g. MANY Facebook USERS IN THE MIDDLE EAST SEEM TO
BE HIGHLY CONCERNED ABOUT PRIVACY. SCANDINAVIAN USERS ARE THE
LEAST PRIVACY CONCERNED. CANADA REGIONS SHOW UP AT BOTH ENDS,
CLEARLY SPLITTING INTO ENGLISH AND FRENCH SPEAKING PARTS.
B. Privacy awareness
We also collected the privacy settings Q
v
for each node v.
Q
v
consists of four bits, each corresponding to one privacy
attribute. By default, Facebook sets these attributes to ‘al-
low’, i.e., Q
v
= 1111 for a new node v. We call users who
change these default settings as ‘privacy aware’ users, and we
denote by P A the level of privacy awareness of a user v, i.e.,
privacy aware users have P A = P(Q
v
6=1111).
We studied the privacy awareness in Facebook and we
report some of our findings. First, we present the distribution
of privacy settings among Facebook users in Fig. 15, which
shows that about 84% of users leave the settings unchanged,
i.e., P(Q
v
= 1111 ) ≃ 0.84. The remaining 16% of users
modified he default settings, yielding P A = 0.16 across the
entire Facebook. The two most popular modifications are
Q
v
= 1011 (“hide my photo”) and Q
v
= 1101 (“hide my
friends”), each applied by about 7% of users. Second, the
privacy awareness P A of Facebook users depends on many
factors, such as the geographical location, node degree or the
privacy awareness of friends. In Table IV we classify the
regional networks with respect to P A of their members. In
Fig. 16, we show the effect of node degree on the privacy
settings of a user. We found that low degree nodes tend
to be very concerned about privacy, whereas high degree
nodes hardly ever bother to modify the default settings. This
clear trend makes sense in practice: to protect her privacy, a
privacy concerned user would carefully select her Facebook
friends, e.g., by avoiding linking to strangers. At the other
extreme, there are users who prefer to have as many ‘friends’
as possible, which is much easier with unrestricted privacy
attributes. Finally, we found that the privacy awareness of a
P A - privacy awareness
node degree k
Fig. 16. Privacy awareness as a function of node degree in the egonets dataset.
We consider only the nodes with privacy settings set to ’**1*’, because only
these nodes allow us to see their friends and thus degree. So here P A =
P(Q
v
6=1111 | k
v
= k, Q
v
=∗ ∗ 1∗).
P A - privacy awareness
P A - average privacy awareness of node’s neighbors
Fig. 17. Privacy awareness as a function of privacy awareness of node’s
neighbors in the egonets dataset. We consider only the nodes with privacy
settings set to ’**1*’, because only these nodes allow us to see their friends,
so P A = P(Q
v
6=1111 |
P A, Q
v
=∗ ∗ 1∗).
user is positively correlated with the privacy awareness of her
friends. We observe a clear positive correlation in Fig. 17.
VII. CONCLUSION
In this paper, we developed a framework for unbiased
sampling of users in an OSN by crawling the social graph,
and we provided recommendations for its implementation in
practice. We made the following contributions. We compared
several candidate techniques in terms of bias (BFS and RW
were significantly biased, while MHRW and RWRW provided
unbiased samples) and efficiency (we found RWRW to be the
most efficient in practice, while MHRW has the advantage
of providing a ready-to-use sample). We also introduced the
use of formal online convergence diagnostics. In addition,
we performed an offline comparison of all crawling methods
against the ground truth (obtained through uniform sampling
of userIDs via rejection sampling). We also provided guide-
lines for implementing high performance crawlers for sam-
pling OSNs. Finally, we applied these methods to Facebook
and obtained the first unbiased sample of Facebook users,
which we used it to characterize several key user and structural
properties of Facebook. We anonymized our datasets and
made them publicly available at [21]. They have been down-
loaded approximately 500 times at the time of this publication.
15

APPENDIX A: UNIFORM SAMPLE OF USER IDS WITH
REJECTION SAMPLING
In Section III-D we obtained an exact uniform sample of
Facebook users by directly querying the userID space. We
then used it as ground truth for comparing against the samples
collected by the crawling techniques. More specifically, we
used the following procedure:
UNI Sampling Method: First, pick a userID X uniformly
at random in the known range of IDs [0,MAXuserID]. Query
the OSN for user data for the chosen userID X. If the OSN
does not return an error message (i.e., X is valid/allocated),
include X in the sample; otherwise discard it. Repeat the
process.
Note that the userID space is not required to be sequentially
or evenly allocated. In fact, as we explicitly show in Section
V-B3 and Fig.12, the Facebook userID space is not al-
located in a sequential way. Nevertheless, by using rejection
sampling, we are guaranteed to obtain a uniform sample of
the allocated userIDs (not of all userIDs), as the following
proposition indicates.
Proposition: UNI yields a uniform sample of the allocated
user IDs in an Online Social Network.
Proof. Let us consider that there are N allocated
and M non-allocated userIDs in the entire userID space
[0,MAXuserID]. These N and M userIDs do not need to be
consecutive. UNI picks any element, w.p.
1
N+M
and accepts
it if it is valid (w.p. P r{acc epted} =
N
N+M
); otherwise it
rejects it (w.p.
M
N+M
). It is easy to see the distribution of the
accepted userIDs is uniform:
P r{X|accepted} =
1
N
.
Indeed, P r{X|accepted} =
P r{X and accepted}
P r{accepted}
. If the userID is
valid then P r{X|accepted} =
1
N +M
·1
N
N +M
=
1
N
; otherwise it is 0.
The above is just a special case of textbook rejection
sampling (e.g., see [60], Chapter 3), when the desired sam-
pling distribution is uniform. It is only repeated here for
completeness. A common misunderstanding is to interpret
UNI as a uniform sample of the entire userID space, while
it is a uniform sample only of the allocated/valid userIDs,
independently from where in they userID space these IDs may
be.
Limitations. There are some requirements for being able
to implement UNI, which are met in our measurements of
Facebook.
• First, we need to know or estimate the range of userIDs
assigned to users, or equivalently the maximum known
userID, MAXuserID. Since we use rejection sampling,
overestimating MAXuserID simply results to more re-
jections. Knowledge of the actual distribution of userIDs
in the userID space is not needed, as explained above.
• Second, we need to be able to query the OSN to return
data for the selected userID, if it is valid, or return an
P(k
v
= k)
node degree k
(a) Node Degree
P(Q
v
= Q)
Privacy bits Q
(b) Privacy Settings Q
v
Fig. 18. PDF of two user properties for UNI samples obtained 45 days apart
error message if it does not exist. This was supported by
Facebook at the time of our experiment.
• Furthermore, UNI is efficient only if the probability of
acceptance is high. This was the case at the time of our
experiments, when the userID was 32bits, but is no longer
the case now that Facebook switched to 64bit IDs.
We emphasize that we use UNI only as a baseline for
comparing the crawling methods against ground truth.
APPENDIX B: TEMPORAL DYNAMICS
The Facebook friendship graph can be considered practi-
cally static in the timescales our crawls, consistently with our
assumption A4. Facebook is growing in general (as reported
by websites such as [69,70]) but in much longer timescales
than the duration of our crawls (which were in the order of a
few days, thanks to the efficient crawlers we developed). To
confirm that this is indeed the case in Facebook, we took
the following steps.
First, we compared our metrics of interest between the UNI
sample of Table II and a similarly sized UNI sample obtained
45 days later. Fig 18 shows the distribution of node degree
and privacy settings. One can easily observe that the two
distributions we obtained were virtually identical. The same
was true in all other comparisons we did on the same metrics
of interest in the each sample across different days.
Second, during the period that we performed our crawls (see
table II), Facebook was growing at a rate of 450K/day as
reported by websites such as [69,70]. With a population of
∼200M users during that period, this translates to a growth
of 0.22% of users/day. Each of our crawls lasted around
4-7 days (during which, the total Facebook growth was
0.9%-1.5%); in fact, our convergence analysis shows that the
process converged even faster, i.e., in only one day. Therefore,
16

∆k
v
/k
v
∆k
v
k
v
k
v
(a) Relative degree and absolute degree change as a function of node degree
∆k
v
/k
v
∆k
v
(b) Cumulative Distribution Function of relative degree and absolute degree
change
Fig. 19. Daily growth of social graph for five days
the relative node growth of Facebook users was negligible
during our crawls.
Third, we evaluated the edge growth of the Facebook
graph by conducting the following experiment. In November
2010 we ran 20 independent RW crawls and collected 20 ×
10K = 200K user samples within 12 hours. This is our user
sample |S|
0
at Day 0. For the next 5 days, we re-visit the exact
same nodes in the same order and check their edges to see if
there is any change. These will be our user samples |S|
1
..|S|
5
,
at Days 1,..,5 and their collection is approximately equally
spaced in time. Let us define ∆k
day
v
= |k
day
v
− k
0
v
| as the
absolute degree change where day ∈ [1..5] and ∆k
day
v
/k
day
v
as
the relative degree change. Fig 19(a) shows the absolute degree
and relative degree change as a function of node degree for
Days 1,5. We observe that at Day 5 the relative degree change
varies between 0.5%-2% depending on the node degree. In
summary, the total relative change at Day 5 is estimated as
1
|S|
X
v∈ |S|
∆k
d5
v
k
d5
v
which is 1.13%. Fig 19(b) shows the CDF of relative and
absolute degree change for Days 1..5. It can be seen that 50%
and 80% of the users at Day 5 and Day 1 respectively have
an absolute degree change of one or zero. Additionally, 70%
and 95% of the users at Day 5 and Day 1 respectively have a
relative degree change of less than 1%.
Last, and perhaps most importantly, another way to eval-
uate the effect of edge growth in the estimation of the
degree distribution (or any other property) is to compare
1
|S|
P
v∈ |S|
(∆k
d5
v
)
2
, which is the node degree variance due to
temporal dynamics at day 5, to
1
|S|
P
v∈ |S|
(
k − k
d5
v
)
2
, which
is the variance of the node degree distribution at day 5. The
former value is estimated at 556 while the latter at 617, 829,
which makes the node degree variance due to the temporal
dynamics at least three orders of magnitude smaller than the
distribution variance, i.e., essentially noise.
These results are expected, since we deal with the social
graph, which is much more static than other types of graphs,
i.e., the interaction graph on OSNs or P2P graphs [18,41] that
are known to have high churn. In the latter case, considering
the dynamics becomes important. However, they appear not to
be problematic for this particular study.
APPENDIX C: MHRW VS. RWRW
Although both MHRW and RWRW achieve asymptotically
unbiased samples, experimental results on Facebook in
Fig. 9 showed that RWRW outperforms MHRW in terms of
sampling efficiency. This is consistent with what was reported
by Rasti et al. [17] in the context of unstructured peer-to-peer
networks. We investigate this further, by taking the following
steps: (i) we run simulations on a broad range of Internet
topologies, (ii) we attempt to gain more intuition via simplified
analysis, and (iii) we show a counterexample where MHRW
is better than RWRW in a specific pathological case. Our
conclusion is that RWRW is more efficient than MHRW in
most topologies that are likely to arise in practice.
A. Simulation results
We compare RWRW with MHRW on a broad range of large,
real-life, but fully known Internet topologies described in
Table V. As our main source of data we use the SNAP Graph
Library [71]. We show the results in Fig. 20. The number on
the bottom-left corner of every plot indicate how much longer
MHRW should be than RWRW so as to achieve the same error.
One can see that, in all cases, MHRW requires 1.5-7 times
more (unique) samples to achieve the same estimation quality
as RWRW. Recall that in our Facebook measurement, this
advantage of RWRW over MHRW is about 3.0 (see Fig. 9).
B. Intuition
Why does RWRW perform so much better than MHRW on
real-life Internet topologies? There are three aspects that play
a major role here, as discussed below.
1) MHRW strongly re-samples low-degree nodes: By de-
sign, MHRW prefers visiting low-degree nodes over high-
degree ones, which compensates for the node degree bias
observed under RW. However, counter-intuitively, MHRW
does not visit significantly more unique low-degree nodes than
RW does. Instead, it strongly re-samples the already-visited
low-degree nodes. Indeed, under MHRW, the probability of
leaving the node u at any iteration is
p
u
=
X
w∈Neighbors of u
1
k
u
· min(1,
k
u
k
w
) (2)
Therefore, the number of rounds MHRW stays in node u is
a geometric random variable Geom(p
u
) with parameter p
u
and mean 1/p
u
. In some graphs, 1/p
u
may be in the order of
thousands.
17
Dataset nodes edges Description
AS 26K 53K CAIDA AS Relationships Datasets, 2004
Email 225K 341K Email network of a large Institution [72]
WWW 326K 1 118K Web graph of Notre Dame, 1998 [73]
P2P 63K 148K Gnutella p2p network, 08-2002 [72]
Slashdot 77K 546K Slashdot social network, 11-2008 [74]
TABLE V
REAL-LIFE INTERNET TOPOLOGIES USED IN SIMULATIONS. ALL GRAPHS
ARE CONNECTED AND UNDIRECTED (WHICH REQUIRED PREPROCESSING
IN SOME CASES).
2) Re-sampling geometric process introduces variance:
RWRW compensates for the bias of RW by dividing each
measured value of node u by its degree k
u
, which is a
fixed number. In contrast, MHRW achieves it by re-sampling
node u, as shown above, which is a random process on its own
that introduces additional variance. We demonstrate this using
the example below. Consider a star topology with node v
∗
in the middle and nodes V being its one-hop neighbors. Let
V
′
⊂ V be the nodes of some type of interest. Our goal is to
estimate the fraction θ =
|V
′
|
|V |
. To this end, we use RW and
MHRW to collect a sample S ⊂ V of nodes (for simplicity,
we intentionally ignore node v
∗
) of size N = |S|. Clearly, we
can estimate θ by
ˆ
θ =
1
N
X
v∈ S
1
v∈ V
′
.
RW alternates between v
∗
, and nodes chosen from V
uniformly at random, with replacements. Therefore,
ˆ
θ
RW
=
Binom(θ, N )
N
and
V[
ˆ
θ
RW
] =
1
N
2
· V[Binom(θ, N)] =
θ(1 − θ)
N
.
In contrast, MHRW stays at any node from V for some num-
ber of rounds that follow a geometric distribution Geom(q).
In our example, Eq.(2) yields parameter q = 1/|V |. Therefore,
MHRW spends on average |V | rounds at every visited node
from V , which means that MHRW spends a large fraction
of its N samples (fraction
|V |−1
|V |
on average) for re-sampling
the same nodes, which drastically limits the performance of
the MHRW estimator. In practice, however, re-sampling an
already known node is free in terms of required bandwidth.
Therefore, it makes sense to count all consecutive visits as 1
towards the sample size N , which yields
ˆ
θ
MHRW
=
q
N
Binom(θ,N )
X
1
Geom(q).
Because Binom(θ
k
, N ) and Geom(q) are independent, after
some calculations, we get:
V[
ˆ
θ
MHRW
] =
θ(1 − θ)
N
+
θ(1 − q)
N
>
θ(1 − θ)
N
= V[
ˆ
θ
RW
].
3) MHRW avoids high-degree nodes, missing good mixing
opportunities: Finally, in networks that arise in practice, nodes
of high degree are more likely to act as hubs, i.e., to span
averagedegreedegreedistribution fraction0.5
Sample length |S| Sample length |S|Sample length |S|
Fig. 20. Performance of MHRW and RWRW in simulations on Internet
topologies described in Table V. We use MHRW and RWRW to collect
samples. Based on 1000 such samples, we estimate three different graph
parameters (below). We draw the median estimation error of MHRW (red
triangles) and RWRW (green circles) as a function of sample length |S|
counted in unique nodes. (The actual samples include repetitions and are
therefore longer than |S|.) (left) Node degree distribution. Error metric is
the Kolmogorov-Smirnov (KS) statistic, i.e., the max vertical distance between
CDFs. (middle) Average node degree. (right) Fraction f= 0.5 of labeled
nodes. We select at random fraction f= 0.5 of all nodes and use MHRW and
RWRW to estimate f. The numbers in the bottom-left corner of each figure
indicate how much longer MHRW should be than RWRW to achieve the same
error, on average.
different parts of the graph than the low-degree nodes whose
connections are usually more local. Therefore, by avoiding
hubs, MHRW misses mixing opportunities. In contrast, RW
exploits them.
C. Counter-example
Although RW outperformed MHRW on all real-life topolo-
gies we tested, it is not true that RW is always more efficient.
We show one – carefully constructed and rather unrealistic
– counterexample in Fig. 21(a). Here, every node carries a
value equal to its number, and our goal is to estimate the
average value θ (in this example θ = 13). If the sampling
process stays in the clique v
1
. . . v
10
, then the value will
be strongly underestimated (probably resulting in
ˆ
θ ≃ 5.5.
Similarly, staying in the clique v
16
. . . v
25
yields
ˆ
θ ≃ 20.5. In
order to achieve a good estimate
ˆ
θ ≃ θ, our process should
be able to switch between the two cliques.
Inside a clique, say inside v
1
. . . v
10
, RW and MHRW
behave almost identically. The differences appear once we
enter the line section at v
11
. MHRW will typically stay on
18

(a) Tested topology (b) Normalized Root Mean Square Error (NMSE)
Fig. 21. An example where MHRW performs better than RW. (a) Tested
toy graph. It consists of two cliques connected by a 6-hop path. We sample it
with RW and MHRW initiated at random nodes. (b) Normalized Root Mean
Square Error (NMSE) of the estimation of the average node number (true
average is equal to 13), as a function of total sample length. The standard
deviation error bars (not shown) are comparable with the symbol size.
this line for many iterations (which is not good per se), and
eventually end up in one of the cliques with roughly the
same probabilities (which is good). In contrast, RW at v
11
has a much higher chance to return to clique v
1
. . . v
10
, which
significantly slows down mixing and thus harms estimation
performance. Similar reasoning applies when leaving clique
v
16
. . . v
25
at node v
15
. Therefore, MHRW should system-
atically outperform RW in this example. This intuition is
confirmed by the simulation results in Fig. 21(b).
D. Summary
In some pathological cases, like the one presented in Fig. 21,
MHRW may outperform RWRW. In more practical examples,
at least in all real-life topologies we tried, RWRW requires 1.5-
7 times fewer unique samples to achieve the same estimation
quality as MHRW, which directly translates into several-fold
bandwidth gains. For this reason, we strongly recommend
RWRW for sampling nodes in OSN and other Internet topolo-
gies. However, fully characterizing the relation between graph
structure and convergence of MHRW, RWRW is out of the
scope of this paper.
REFERENCES
[1] “Nielsen statistics, June 2010,” http://blog.nielsen.com/nielsenwire/ on-
line
mobile/social-media-accounts-for-22-percent-of-time-online/ .
[2] “Alexa traffic statistics for Facebook, June 2010,”
http://www.alexa.com/siteinfo/facebook.com.
[3] J. Pujol, V. Erramilli, G. Siganos, X. Yang, N. Laoutaris, P. Chhabra,
and P. Rodriguez, “The little engine (s) that could: Scaling online social
networks,” ACM SIGCOMM Computer Communication Review, vol. 40,
no. 4, pp. 375–386, 2010.
[4] S. Agarwal and S. Agarwal, “Social networks as Internet barometers for
optimizing content delivery networks,” in Proc. 3rd IEEE Int. Symp. on
Advanced Networks and Telecommunication Systems, New Delhi, India,
Dec. 2009.
[5] A. Nazir, S. Raza, D. Gupta, C. Chuah, and B. Krishnamurthy, “Network
level footprints of facebook applications,” in Proc. 9th ACM SIGCOMM
Conf. on Internet measurement, New York, NY, 2009, pp. 63–75.
[6] A. Mislove, A. Post, P. Druschel, and K. Gummadi, “Ostra: Leveraging
trust to thwart unwanted communication,” in Proc. 5th USENIX Symp.
on Networked Systems Design and Implementation, San Francisco, CA,
2008, pp. 15–30.
[7] M. Sirivianos, X. Yang, and K. Kim, “SocialFilter: introducing social
trust to collaborative spam mitigation,” in Proc. IEEE INFOCOM,
Shanghai, China, 2011.
[8] M. Sirivianos, K. Kim, and X. Yang, “FaceTrust: Assessing the credibil-
ity of online personas via social networks,” in Proc. 4th USENIX Conf.
on Hot topics in security, Montreal, Canada, 2009.
[9] Y. Ahn, S. Han, H. Kwak, S. Moon, and H. Jeong, “Analysis of
topological characteristics of huge online social networking services,”
in Proc. 16th Int. Conf. on World Wide Web, Banff, Alberta, Canada,
2007, pp. 835–844.
[10] J. Leskovec, L. Backstrom, R. Kumar, and A. Tomkins, “Microscopic
evolution of social networks,” in Proc. 14th ACM SIGKDD Int. Conf.
on Knowledge discovery and data mining, Las Vegas, NV, 2008.
[11] K. Lewis, J. Kaufman, M. Gonzalez, A. Wimmer, and N. Christakis,
“Tastes, ties, and time: A new social network dataset using Facebook.
com,” Social Networks, pp. 330–342, 2008.
[12] A. Mislove, M. Marcon, K. Gummadi, P. Druschel, and B. Bhattacharjee,
“Measurement and analysis of online social networks,” in Proc. 7th ACM
SIGCOMM Conf. on Internet measurement, San Diego, CA, 2007, pp.
29–42.
[13] C. Wilson, B. Boe, A. Sala, K. Puttaswamy, and B. Zhao, “User
interactions in social networks and their implications,” in Proc. 4th ACM
European Conf. on Computer systems, Nuremberg, Germany, 2009, pp.
205–218.
[14] M. Kurant, A. Markopoulou, and P. Thiran, “On the bias of BFS
(Breadth First Search),” in Proc. 22nd Int. Teletraffic Congr., also in
arXiv:1004.1729, 2010.
[15] ——, “Towards Unbiased BFS Sampling,” To appear in IEEE J. Sel.
Areas Commun. on Measurement of Internet Topologies, 2011.
[16] M. Salganik and D. D. Heckathorn, “Sampling and estimation in hidden
populations using respondent-driven sampling,” Sociological Methodol-
ogy, vol. 34, no. 1, pp. 193–240, 2004.
[17] A. Rasti, M. Torkjazi, R. Rejaie, N. Duffield, W. Willinger, and
D. Stutzbach, “Respondent-driven sampling for characterizing unstruc-
tured overlays,” in Proc. IEEE INFOCOM Mini-conference, Rio de
Janeiro, Brazil, 2009, pp. 2701–2705.
[18] D. Stutzbach, R. Rejaie, N. Duffield, S. Sen, and W. Willinger, “On
unbiased sampling for unstructured peer-to-peer networks,” in Proc. 6th
ACM SIGCOMM Conf. on Internet measurement, Rio de Janeiro, Brazil,
2006.
[19] A. H. Rasti, M. Torkjazi, R. Rejaie, and D. Stutzbach, “Evaluating
Sampling Techniques for Large Dynamic Graphs,” Univ. Oregon, Tech.
Rep. CIS-TR-08-01, Sep. 2008.
[20] B. Krishnamurthy, P. Gill, and M. Arlitt, “A few chirps about twitter,”
in Proc. 1st workshop on Online social networks, Seattle, WA, 2008,
pp. 19–24.
[21] “Uniform Sampling of Facebook Users: Publicly Available Datasets,
2009,” http://odysseas.calit2.uci.edu/osn.
[22] S. Wasserman and K. Faust, Social Network Analysis: Methods and
Applications. Cambridge University Press, 1994.
[23] A. Mislove, H. Koppula, K. Gummadi, P. Druschel, and B. Bhattachar-
jee, “Growth of the flickr social network,” in Proc. 1st workshop on
Online social networks, Seattle, WA, 2008, pp. 25–30.
[24] B. Viswanath, A. Mislove, M. Cha, and K. Gummadi, “On the evolution
of user interaction in facebook,” in Proc. 2nd workshop on Online social
networks, Barcelona, Spain, 2009, pp. 37–42.
[25] S. H. Lee, P.-J. Kim, and H. Jeong, “Statistical properties of sampled
networks,” Physical Review E, vol. 73, p. 16102, 2006.
[26] L. Becchetti, C. Castillo, D. Donato, A. Fazzone, and I. Rome, “A
comparison of sampling techniques for web graph characterization,” in
Proc. Workshop on Link Analysis, Philadelphia, PA, 2006.
[27] S. Ye, J. Lang, and F. Wu, “Crawling online social graphs,” in Proc.
12th Asia-Pacific Web Conference, Busan, Korea, 2010, pp. 236–242.
[28] L. Lov´asz, “Random walks on graphs: A survey,” Combinatorics, Paul
Erdos is Eighty, vol. 2, no. 1, pp. 1–46, 1993.
[29] M. R. Henzinger, A. Heydon, M. Mitzenmacher, and M. Najork, “On
near-uniform URL sampling,” in Proc. 9th Int. Conf. on World Wide
Web, Amsterdam, Netherlands, 2000.
[30] E. Baykan, M. Henzinger, S. Keller, S. De Castelberg, and M. Kinzler,
“A comparison of techniques for sampling web pages,” in Proc. 26th Int.
19
Symp. on Theoretical Aspects of Computer Science, Freiburg, Germany,
2009.
[31] C. Gkantsidis, M. Mihail, and A. Saberi, “Random walks in peer-to-peer
networks,” in Proc. IEEE INFOCOM, Hong Kong, China, 2004.
[32] J. Leskovec and C. Faloutsos, “Sampling from large graphs,” in Proc.
12th ACM SIGKDD Int. Conf. on Knowledge discovery and data mining,
Philadelphia, PA, 2006, pp. 631–636.
[33] K. Avrachenkov, B. Ribeiro, and D. Towsley, “Improving Random
Walk Estimation Accuracy with Uniform Restarts,” in I7th Workshop
on Algorithms and Models for the Web Graph, 2010.
[34] B. Ribeiro and D. Towsley, “Estimating and sampling graphs with
multidimensional random walks,” in Proc. 10th ACM SIGCOMM Conf.
on Internet measurement, Melbourne, Australia, 2010.
[35] M. Kurant, M. Gjoka, C. T. Butts, and A. Markopoulou, “Walking on
a Graph with a Magnifying Glass: Stratified Sampling via Weighted
Random Walks,” in Sigmetrics, 2011.
[36] M. Gjoka, C. T. Butts, M. Kurant, and A. Markopoulou, “Multigraph
Sampling of Online Social Networks,” To appear in IEEE J. Sel. Areas
Commun. on Measurement of Internet Topologies, 2011.
[37] M. Latapy and C. Magnien, “Complex network measurements: Estimat-
ing the relevance of observed properties,” in Proc. IEEE INFOCOM,
Phoenix, AZ, 2008, pp. 1660–1668.
[38] R. Kumar, J. Novak, and A. Tomkins, “Structure and Evolution of Online
Social Networks,” in Proc. 12th ACM SIGKDD Int. Conf. on Knowledge
discovery and data mining, Philadelphia, PA, 2006.
[39] L. Backstrom, D. Huttenlocher, J. Kleinberg, and X. Lan, “Group For-
mation in Large Social Networks: Membership, Growth, and Evolution,”
in Proc. 12th ACM SIGKDD Int. Conf. on Knowledge discovery and data
mining, Philadelphia, PA, 2006.
[40] P. Sarkar and A. W. Moore, “Dynamic social network analysis using
latent space models,” ACM SIGKDD Explorations Newsletter, vol. 7,
no. 2, pp. 31–40, Dec. 2005.
[41] W. Willinger, R. Rejaie, M. Torkjazi, M. Valafar, and M. Maggioni,
“OSN Research: Time to face the real challenges,” in Proc. of 2nd
Workshop on Hot Topics in Measurement & Modeling of Computer
Systems, Seattle, WA, 2009.
[42] E. D. Kolaczyk, “Statistical Analysis of Network Data,” Springer Series
in Statistics, vol. 69, no. 4, 2009.
[43] M. Stumpf, C. Wiuf, and R. May, “Subnets of scale-free networks are not
scale-free: sampling properties of networks,” Proc. of the Nat. Academy
of Sciences of the United States of America, vol. 102, no. 12, p. 4221,
Mar. 2005.
[44] B. Krishnamurthy, “A measure of online social networks,” in Proc. 1st
Int. Conf. on Communication Systems and Networks, Bangalore, India,
Jan. 2009.
[45] M. A. Porter, “Facebook5 data,” http://www.insna.org/software/data.html,
2008.
[46] B. Krishnamurthy and C. Wills, “Characterizing privacy in online social
networks,” in Proc. 1st workshop on Online social networks, Seattle,
WA, 2008, pp. 37–42.
[47] J. Bonneau, J. Anderson, R. Anderson, and F. Stajano, “Eight friends
are enough: Social graph approximation via public listings,” in Proc.
EuroSys Workshop on Social Network Systems, Nuremberg, Germany,
2009, pp. 13–18.
[48] M. Gjoka, M. Sirivianos, A. Markopoulou, and X. Yang, “Poking
Facebook: characterization of OSN applications,” in Proc. 1st workshop
on Online social networks, Seattle, WA, 2008, pp. 31–36.
[49] D. Liben-Nowell, J. Novak, R. Kumar, P. Raghavan, and A. Tomkins,
“Geographic routing in social networks,” Proc. of the Nat. Academy of
Sciences of the United States of America, vol. 102, no. 33, p. 11623,
2005.
[50] M. Cha, H. Kwak, P. Rodriguez, Y.-Y. Ahn, and S. Moon, “I Tube, You
Tube, Everybody Tubes: Analyzing the World’s Largest User Generated
Content Video System,” in Proc. 7th ACM SIGCOMM Conf. on Internet
measurement, San Diego, CA, 2007.
[51] P. Gill, M. Arlitt, Z. Li, and A. Mahanti, “Youtube traffic characteri-
zation: a view from the edge,” in Proc. 7th ACM SIGCOMM Conf. on
Internet measurement, San Diego, CA, 2007.
[52] M. Gjoka, M. Kurant, C. T. Butts, and A. Markopoulou, “Walking in
Facebook: A Case Study of Unbiased Sampling of OSNs,” in Proc. IEEE
INFOCOM, San Diego, CA, 2010.
[53] B. Ribeiro, P. Wang, and D. Towsley, “On Estimating Degree Distribu-
tions of Directed Graphs through Sampling,” UMass, Tech. Rep. UM-
CS-2010-046, 2010.
[54] J. Haupt, W. Bajwa, M. Rabbat, and R. Nowak, “Compressed sensing
for networked data,” IEEE Signal Processing Mag., vol. 25, no. 2, pp.
92–101, 2008.
[55] M. Kurant, M. Gjoka, Y. Wang, Z. W. Almquist, C. T. Butts, and
A. Markopoulou, “Coarse-Grained Topology Estimation via Graph Sam-
pling,” Arxiv preprint arXiv:1105.5488, 2011.
[56] M. Hansen and W. Hurwitz, “On the Theory of Sampling from Finite
Populations,” Annals of Mathematical Statistics, vol. 14, no. 3, 1943.
[57] E. Volz and D. D. Heckathorn, “Probability based estimation theory for
respondent driven sampling,” Journal of Official Statistics, vol. 24, no. 1,
pp. 79–97, 2008.
[58] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and
E. Teller, “Equation of state calculation by fast computing machines,”
Journal of Chemical Physics, vol. 21, pp. 1087–1092, 1953.
[59] W. R. Gilks, S. Richardson, and D. J. Spiegelhalter, Markov Chain Monte
Carlo in Practice. Chapman and Hall/CRC, 1996.
[60] A. Leon-Garcia, Probability, statistics, and random processes for elec-
trical engineering. Pearson/Prentice Hall, 2008.
[61] “Facebook announcement on 64 bit userIDs, May 2009,”
http://developers.facebook.com/blog/post/226.
[62] J. Geweke, “Evaluating the accuracy of sampling-based approaches to
the calculation of posterior moments,” in Bayesian Statistics, 1992, pp.
169–193.
[63] A. Gelman and D. Rubin, “Inference from iterative simulation using
multiple sequences,” in Statistical science, vol. 7, no. 4, 1992, pp. 457–
472.
[64] “The facebook blog: Growing beyond regional networks, June 2009,”
http://blog.facebook.com/blog.php?post=91242982130.
[65] “Facebook’s userID numbering system,”
http://www.quora.com/What-is-the-history-of-Facebooks-ID-numbering-system.
[66] D. Rubin, “Using the SIR algorithm to simulate posterior distributions,”
in Bayesian Statistics, 1988, vol. 3, pp. 395–402.
[67] O. Skare, E. Bø lviken, and L. Holden, “Improved Sampling-Importance
Resampling and Reduced Bias Importance Sampling,” in Scandinavian
Journal of Statistics, 2003, vol. 30, no. 4, pp. 719–737.
[68] M. Newman, “Assortative mixing in networks,” Physical Review Letters,
vol. 89, no. 20, p. 208701, 2002.
[69] “Facebook statistics, Dec 2010,” http://facebook.com/press/info.php?statistics.
[70] “Inside facebook, July 2009,” http://www.insidefacebook.com/2009/07/02/
facebook-now-growing-by-over-700000-users-a-day-updated-
engagement-stats/ .
[71] “SNAP Graph Library,” http://snap.stanford.edu/data/.
[72] J. Leskovec, J. Kleinberg, and C. Faloutsos, “Graph evolution: Den-
sification and shrinking diameters,” ACM Transactions on Knowledge
Discovery from Data, vol. 1, no. 1, p. 2, Mar. 2007.
[73] R. Albert, H. Jeong, and A. Barab´asi, “Diameter of the world-wide web,”
Nature, vol. 401, no. 6749, pp. 130–131, 1999.
[74] J. Leskovec, K. Lang, A. Dasgupta, and M. Mahoney, “Community
structure in large networks: Natural cluster sizes and the absence of
large well-defined clusters,” Internet Mathematics, vol. 6, no. 1, pp. 29–
123, 2009.
20
